14 de agosto de 2014
No final da semana passada, a DGES revelou o número de candidatos ao Ensino Superior (candidaturas à 1.ª fase do concurso nacional). Há cerca de dois anos que ando a tentar ver, ano a ano, se se consegue prever o número de candidatos para se poderem definir melhor as vagas no Ensino Superior público (Partes I, II, e III). No mês passado, depois de ser a lançada a nota do exame nacional de Matemática A, usando o modelo com os dados dos anos anteriores, previ um intervalo de confiança (99%) de entre 37.431 a 42.510 candidatos. Segundo a DGES o valor final, este ano foi de 42.455, praticamente no limite superior do intervalo. No ano passado já tinha verificado a validade do modelo à posteriori, este ano consegui prever o número de candidatos.
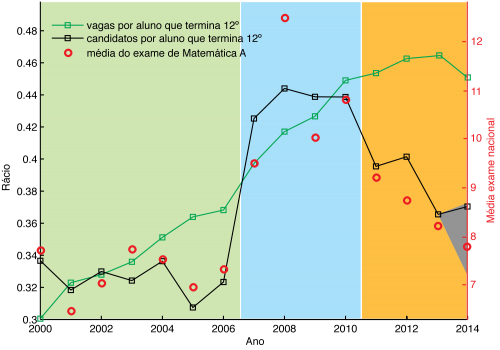
Segundo o MEC há 50.820 vagas, 1,2% a menos que no ano passado. Deste modo, com uma ligeira descida do número de vagas e um ligeiro aumento dos candidatos, o diferencial entre candidatos e vagas começa finalmente a descer, sendo que ficarão por preencher 8365 vagas, cerca de 16% do total.
A correlação entre a média dos exames de Matemática A e o rácio do número de candidatos por finalistas (segundo o meu modelo) parece manter-se relativamente robusta. Ou seja, $$ R = p_{1} \times média + p_2 $$ em que \(p_1 = 0.0278\), \(p_2 = 0.1334\) (baseados nos valores de 2000 a 2013) e \(R=\frac{candidatos}{finalistas}\).
Revisitando a minha questão original – tentar construir um modelo que previsse o número de candidatos ao Ensino Superior – a versão actual do meu modelo é então: $$ candidatos = \left( p_{1} \times média + p_2 \right) \times finalistas $$ sendo que os \(finalistas\) do 12º ano são calculados através da propagação dos nascimentos pelos anos de escolaridade, com dois parâmetros que modelam as reprovações e a passagem do Ensino Básico para o Secundário. Esses parâmetros estão descritos em detalhe na Parte I.
Outra forma alternativa de mostrar a mesma informação é precisamente desenhar um gráfico da equação anterior, em que os factores de correcção dados pela correlação (e que variam, ano a ano, consoante a média do exame de Matemática A) ajustam os valores calculados do número de alunos que terminam o Ensino Secundário (para os anos futuros, assumi uma média de 8,5 valores). Os resultados estão representado na linha azul. Como se pode ver, estão muito próximos dos valores oficiais (a preto), o que é já era esperado dada a correlação que encontrei. Ainda não arranjei forma de comparar a minha determinação de alunos finalistas com dados oficiais, mas cada vez mais me parece que a minha estimativa deve estar próxima da realidade, se não em números absolutos, pelo menos na tendência relativa.
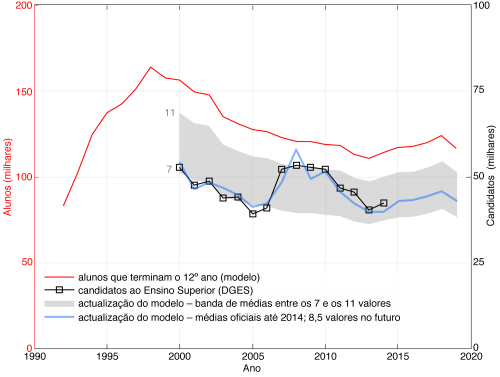
A reacção oficial aos números de candidatos deste ano congratulou-se pelo aumento de candidatos. Se o meu modelo estiver correcto, este ligeiro aumento deveu-se sobretudo a tendências demográficas, já que o nível de facilidade do exame de Matemática A se manteve semelhante ao ano passado. No Público, o jornalista afirma:
Este resultado significa uma inversão na tendência de quebra da procura que se registava desde 2008, pelo que o presidente da Comissão Nacional de Acesso ao Ensino Superior (CNAES) acredita que a conjuntura negativa no sector está a ser ultrapassada.
Caro jornalista Samuel Silva: isto não é necessariamente uma inversão de tendência. Uma tendência necessita que haja qualquer coisa que tenda para um lado ou para o outro, por definição, logo uma flutuação não muda necessariamente a tendência. Veja-se, no gráfico acima, o número de candidatos entre 2000 e 2006, com tendência claramente de decrescimento. No entanto, em 2002, 2004 e 2006 houve valores que foram maiores que nos anos anteriores, sem que isso se tenha traduzido numa alteração da tendência. Quanto muito a inversão deu-se em 2006, mas isso só foi possível ser afirmado em 2007.
A crer no meu modelo, no entanto, o jornalista poderá vir a ter razão. Se as médias se mantiverem, e, mais ainda, se aumentarem, há razão para que haja, nos próximos 5 anos, uma ligeira tendência de aumento dos candidatos (qualquer coisas como 7500 a 12500 candidatos a mais, daqui a 5 anos, dependendo da facilidade dos exames). Parece que os factores demográficos estão a dar o último fôlego ao sistema:
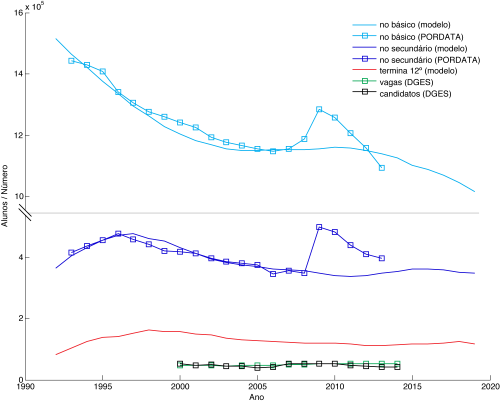
A pequena bossa de alunos no Básico no início desta década está agora a passar para pelo Secundário. Note-se que o meu modelo não entra em linha de conta com os efeitos do programa Novas Oportunidades (os desvios enormes, iniciados em 2009, nos dados oficiais da Pordata, mas que nunca observei traduzirem-se em mais alunos a irem para a faculdade). De facto, depois de 2015 a tendência decrescente de alunos no Ensino Básico é assustadora. Essa tendência passará para o Secundário e depois para o Ensino Superior. De notar que só cerca de 50% dos alunos que acabam o Ensino Secundário é que se candidatam ao Superior. Há aí margem para combater a demografia, mas em termos de futuro demográfico do país é meramente um paleativo.